Coeficiente de correlación de Pearson

En estadística, el coeficiente de correlación de Pearson es una medida de dependencia lineal entre dos variables aleatorias cuantitativas. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de medida de las variables.

De manera menos formal, podemos definir el coeficiente de correlación de Pearson como un índice que puede utilizarse para medir el grado de relación de dos variables siempre y cuando ambas sean cuantitativas y continuas.

Definición

Para una población

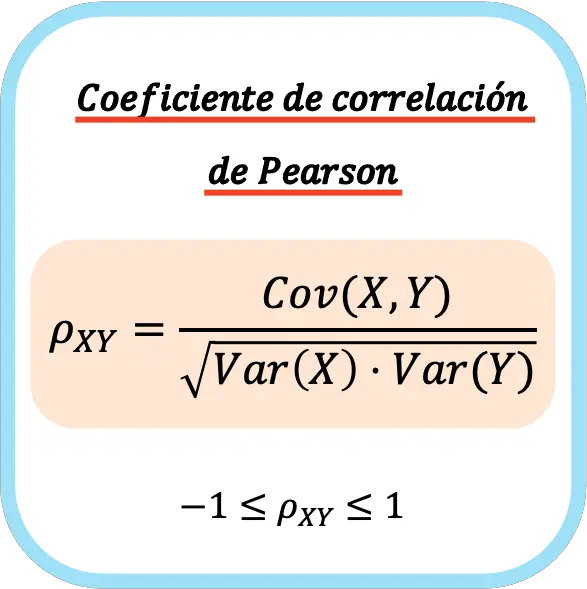
El coeficiente de correlación de Pearson cuando se aplica a una población típicamente se representa por la letra griega ${\displaystyle \rho }$ (rho) y se refiere a ella coeficiente de correlación poblacional o el coeficiente de correlación poblacional de Pearson.

Dado un par de variables aleatorias ${\displaystyle (X,Y)}$, el coeficiente de correlación poblacional de Pearson (también denotado por ${\displaystyle \rho _{X,Y}}$) se define como

${\displaystyle \rho _{X,Y}={\sigma _{XY} \over \sigma _{X}\sigma _{Y}}={\frac {\operatorname {Cov} (X,Y)}{\sqrt {\operatorname {Var} (X)\operatorname {Var} (Y)}}}}$

donde

• ${\displaystyle \sigma _{XY}}$ es la covarianza de ${\displaystyle (X,Y)}$
• ${\displaystyle \sigma _{X}}$ es la desviación estándar de la variable ${\displaystyle X}$
• ${\displaystyle \sigma _{Y}}$ es la desviación estándar de la variable ${\displaystyle Y}$

Para una muestra

El coeficiente de correlación de Pearson cuando es aplicado a una muestra, se suele denotar por ${\displaystyle r_{xy}}$ y se refiere a este como el coeficiente de correlación muestral o el coeficiente de correlación muestral de Pearson. Dados ${\displaystyle n}$ pares de datos ${\displaystyle \{(x_{i},y_{i})\}_{i=1}^{n}}$, se define el coeficiente de correlación muestral de Pearson como

${\displaystyle r_{xy}={\frac {\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)\left(y_{i}-{\bar {y}}\right)}{{\sqrt {\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}{\sqrt {\sum _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}}}}}}$

donde

• ${\displaystyle n}$ es el tamaño de la muestra.
• ${\displaystyle x_{i},y_{i}}$ son puntos muestrales individuales indexados con ${\displaystyle i}$.
• ${\displaystyle {\bar {x}}}$ denota la media muestral definida por ${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ (análogamente para ${\displaystyle {\bar {y}}}$).

El coeficiente de correlación muestral también puede ser escrito como

${\displaystyle r_{xy}={\frac {n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{{\sqrt {n\sum x_{i}^{2}-(\sum x_{i})^{2}}}~{\sqrt {n\sum y_{i}^{2}-(\sum y_{i})^{2}}}}}.}$

Interpretación

El valor del índice de correlación varía en el intervalo ${\displaystyle [-1,1]}$, indicando el signo el sentido de la relación:

• Si ${\displaystyle r=1}$, existe una correlación positiva perfecta. El índice indica una dependencia total entre las dos variables denominada relación directa: cuando una de ellas aumenta, la otra también lo hace en proporción constante.
• Si ${\displaystyle 0$ entonces existe una correlación positiva.
• Si ${\displaystyle r=0}$ entonces no existe relación lineal pero esto no necesariamente implica que las variables son independientes: pueden existir todavía relaciones no lineales entre las dos variables.
• Si ${\displaystyle -1$, existe una correlación negativa.
• Si ${\displaystyle r=-1}$, existe una correlación negativa perfecta. El índice indica una dependencia total entre las dos variables llamada relación opuesta: cuando una de ellas aumenta, la otra cambia su signo en proporción constante.

Véase también

• Covarianza
• Correlación
• Coeficiente de determinación
• Regresión
• Coeficiente de correlación de Spearman

Enlaces externos

• Correlación de Pearson en el Departamento de Psicología de la Universidad de Oviedo.
• Weisstein, Eric W. «Correlation Coefficient». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.